Bayesian methods are becoming more common in clinical trials. Previously, a lack of computing in sample size software hindered the use of these methods, but improvements in the area have led to more widespread use. To examine what’s new and different about Bayesian sample size determination, we first need to consider what’s done in a traditional setting.

The Traditional Approach
In a traditional Frequentist setting, a hypothesis test is used to determine if there is a statistically significant treatment effect between a new treatment and a control. A sample size is usually chosen to be large enough so that the required power is just reached, for a pre-specified value of the treatment effect. The power of the test (often set to 80 or 90%) is the probability that the study will be able to detect a difference between the new treatment and the control, given the true difference is greater than or equal to the pre-specified value of the treatment effect.
The drawback to this approach is that there is no certainty that the true effect of the treatment is as large as the pre-specified value of the treatment effect. With the clinical trial still in the planning stages, this true effect size is not concretely known. With this in mind, power does not tell us the overall probability of the trial finding a significant effect given this uncertainty, but only the probability of the trial finding a significant effect if the assumed effect size is exactly correct.
Sensitivity Analysis and Sample Size
The traditional approach to solving this problem of uncertainty would often involve completing a sensitivity analysis. Sensitivity analysis can be performed by varying the assumed effect size over some plausible range to assess the effect on the sample size, but some of these possible effect sizes are realistically more likely to be true than others.
Bayesian Assurance: The alternative to traditional power
Bayesian sample size estimation attempts to get around this issue, by allowing for uncertainty around the treatment effect or other assumed parameters.
“Bayesian Assurance” is an alternative to power. In this type of calculation, instead of assuming one specific treatment effect, prior knowledge of the effect size or other parameters can be included in the form of a distribution based on historical data or expert knowledge, or some mix of both. The assurance is the prior expectation of power averaged across possible effect sizes. It can also be thought of as the unconditional probability of the trial finding a significant effect, i.e. not dependent on the effect size equaling one specific value.
Bayesian Assurance - The True Probability of Success
In one way, Bayesian assurance gives us the true “probability of success” of the trial, which may give a more robust insight to the practical utility of the trial. For pharmaceutical companies with many possible chemicals and treatments to put forward for clinical trials, it can be very beneficial to know which treatments may result in the highest probability of a successful clinical trial. In the words of Chuang-Stein et. al. (2010) “Assurance should be a major consideration when designing a confirmatory trial.”
Credible Interval and Confidence Interval
Bayesian analysis also provides an analogue to the traditional confidence interval in the form of a credible interval, to express how well a parameter such as an effect size can be estimated. Estimating parameters via intervals has been suggested in many medical journals, and the reporting of credible intervals has been encouraged by the FDA. In determining sample size for a traditional confidence interval, a single estimate for the standard deviation of the parameter of interest (such as an effect size) is used.
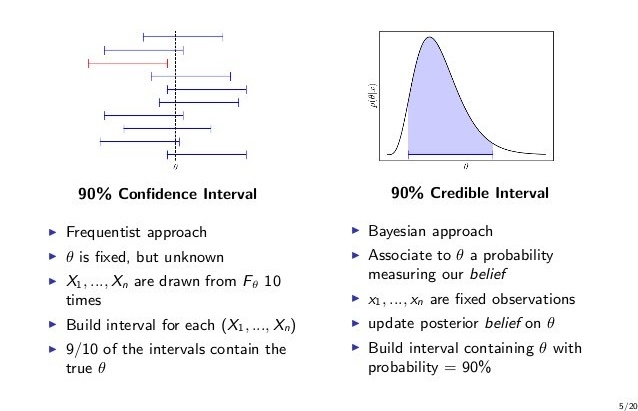
This makes the confidence interval sensitive to the choice of standard deviation. Credible intervals allow input of the standard deviation in the form of a distribution, based on prior information, which can account for uncertainty about the exact value of the parameter. The resulting intervals can be slightly more intuitive than a traditional confidence interval. It can be stated that “there is 95% (or chosen confidence level) probability that the true value of the effect size (or other parameter of choice) lies between the limits of the credible interval”.
Using prior information in this way can reduce sample size compared to taking a traditional Frequentist approach.
Dose Finding Trials
Bayesian analysis can also be used in dose finding trials, designed to identify the dose that is associated with a specific probability of a toxic response. The Bayesian continual reassessment method (CRM) is becoming more common for Phase I clinical trials. The aim is to balance efficacy and toxicity by using a dose-toxicity model and choosing a targeted toxicity level in advance. The model is used to find the maximum tolerated dose (MTD).
In the CRM, a patient is given a particular dose, the outcome is evaluated, and the dose-response relationship is updated. The next patient is given the updated estimate of the MTD. Again, as in other Bayesian methods, the probability of toxicity at each stage in the dose-toxicity model is given a prior distribution. This prior is based on historical data or expert opinion and is then used in estimating the dose level that achieves the target toxicity level. The CRM has been found to provide better results for MTD than the 3+3 design, as more patients are given a dosage close to the MTD. It also has the benefit of a potential efficacy assessment, and makes the study design more suited to formal process and planning.
Conclusion
Bayesian analysis provides us the opportunity to make use of all available information. These methods give mathematically sounds formats for combining information gathered before the trial with new information at all stages in the trial process, from design to analysis.
Each of these methods can be explored through nQuery - the worlds leading sample size software, where sample size for many different variations of study design can be calculated.
Interested in learning more about Bayesian Assurance?
We recently hosted a webinar Bayesian Approaches to Interval Estimation & Hypothesis testing. You can watch this webinar on-demand by clicking the image below.























Comments (1)